Key facts
- Multichannel signal analysis
- Novel internal multipath architecture with cross-correlation
- Preselected I/Q analysis in the microwave range
- 8 GHz internal analysis bandwidth
- Highest level accuracy over the full frequency range




Key facts
FSWX signal and spectrum analyzer
In today’s fast-paced technological landscape, having a reliable and efficient signal analysis solution that can transcend the limits and overcome the limitations of traditional measurement methods is crucial. The cutting-edge multipath FSWX architecture brings a new level of performance and precision to signal analysis. By applying preselection, suppressing inherent noise and spurious signals and minimizing unwanted artifacts, the FSWX ensures that the true characteristics of the signal under test are accurately captured and analyzed.
Quick links
Phase coherent capture at the same or at different frequencies
The ability to capture wideband, modulated phase coherent signals at the same or different frequencies opens up new measurement scenarios. The FSWX is the first multichannel signal and spectrum analyzer to do so.
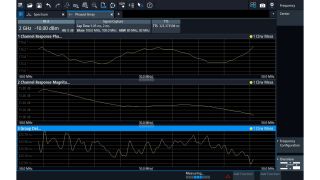
Multiple input ports allow for phase coherent capture of multiple signals. This example shows a comparison of the amplitude and phase of two phased array antenna ports as well as the group delay.
Measure noise level down to the physical limit
The FSWX is the first signal and spectrum analyzer with cross-correlation. Cross-correlation cancels the inherent noise of the analyzer and gives a clear view on the device under test. With cross-correlation, you can push the noise level down to the physical limit for higher dynamic range in noise, phase noise and EVM measurements or spur searches. Benefits include:
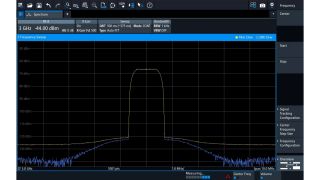
Cross-correlation eliminates the analyzer’s inherent noise and provides an unobstructed view of the signal. Without cross-correlation, the spectrum re-growth of the amplifier under test would not be visible in this example.
Up to 8 GHz analysis bandwidth
The FSWX has been designed as a wide bandwidth instrument. Each analog signal path is terminated by high-resolution, high-speed ADCs providing 8 GHz of analysis bandwidth. This concept includes:
Default filter banks with optional YIG preselector
The FSWX features filter banks with independent highpass and lowpass filters across the whole instrument frequency range. Benefits of filter banks vs swept preselection filters include:
Order number 1348.0000.21
Order number 1348.0000.22
Order number 1348.0000.41
Order number 1348.0000.42
Order number 1347.5443.26
YIG preselection
for FSWX 26.5 GHz models
Order number 1347.5443.44
YIG preselection
for FSWX 44 GHz models
Order number 1348.3580.02
Additional interfaces
Order number 1347.5543.02
Spare CF express card
(R&S®FSW3-B20 option required)
Order number 1349.0110.02
Internal SSD card drive
Order number 1347.5572.02
Removable CF express card drive
Order number 1348.4492.02
Default temperature range
(Default option)
Order number 1348.4505.03
Enhanced temperature range
Order number 1348.4511.02
Default CPU board
(Default option)
Order number 1348.4528.02
Enhanced CPU board
Order number 1348.6450.02
OCXO precision reference frequency
Order number 1347.5537.21
B15X hardware extension for FSWX3026 signal analyzer, 1RF
(mandatory option)
Order number 1347.5537.22
B15X hardware extension for FSWX3026 signal analyzer, 2RF
(mandatory option)
Order number 1347.5537.41
B15X hardware extension for FSWX3044 signal analyzer, 1RF
(mandatory option)
Order number 1347.5537.42
B15X hardware extension for FSWX3044 signal analyzer, 2RF
(mandatory option)
Order number 1348.1093.02
Enhanced electronic attenuator ranging, 1RF
Order number 1348.1106.02
Enhanced electronic attenuator ranging, 2RF
Order number 1347.5495.42
Resolution bandwidth up to 300 MHz, 2RF
Order number 1347.5595.21
RF preamplifier 20 dB 100 Hz to 26.5 GHz
for FSWX3026 1RF-model
Order number 1347.5595.22
RF preamplifier 20 dB 100 Hz to 26.5 GHz
for FSWX3026 2RF model
Order number 1347.5595.41
RF preamplifier 20 dB 100 Hz to 44 GHz
for FSWX3044 1RF-model
Order number 1347.5595.42
RF preamplifier 20 dB 100 Hz to 44 GHz
for FSWX3044 2RF model
Order number 1347.5672.02
100 MHz signal analysis bandwidth, 1RF
Order number 1347.5689.02
100 MHz signal analysis bandwidth, 2RF
Order number 1347.5708.02
320 MHz signal analysis bandwidth, 1RF
Order number 1347.5714.02
320 MHz signal analysis bandwidth, 2RF
Order number 1347.5737.02
600 MHz signal analysis bandwidth, 1RF
Order number 1347.5743.02
600 MHz signal analysis bandwidth, 2RF
Order number 1347.5766.02
1.2 GHz signal analysis bandwidth, 1RF
Order number 1347.5772.02
1.2 GHz signal analysis bandwidth, 2RF
Order number 1347.5795.02
2 GHz signal analysis bandwidth, 1RF
Order number 1347.5808.02
2 GHz signal analysis bandwidth, 2RF
Order number 1347.5820.02
4 GHz signal analysis bandwidth, 1RF
Order number 1347.5837.02
4 GHz signal analysis bandwidth, 2RF
Order number 1347.5850.02
6 GHz signal analysis bandwidth, 1RF
Order number 1347.5866.02
6 GHz signal analysis bandwidth, 2RF
6 GHz ABW only available on 1 RF channel. Max. 4 GHz ABW on each channel with 2 RF channels active
Order number 1347.5889.02
8 GHz signal analysis bandwidth, 1RF
Order number 1347.5895.02
8 GHz signal analysis bandwidth, 2RF
8 GHz ABW only available on 1 RF channel. Max. 4 GHz ABW on each channel with 2 RF channels active
Order number 1347.7600.02
I/Q spectrum analyzer
Order number 1347.7646.02
AM/FM/PM modulation analysis
Order number 1347.7675.02
Amplifier measurements
Order number 1347.7698.02
Frequency response measurements
(R&S®FSW3-KM118 option required)
Order number 1347.7681.02
Direct DPD measurements
(R&S®FSW3-KM118 option required)
Order number 1347.7723.02
Noise figure measurements
Order number 1347.7730.02
Cross-correlation for noise figure measurements
(R&S®FSW3-KM125 option required)
Order number 1347.7752.02
Phase noise measurements
Order number 1347.7769.02
Cross-correlation for phase noise measurements
(R&S®FSW3-KM129 option required)
Order number 1349.2170.02
Cross correlation for I/Q spectrum analyzer
Order number 1349.2129.02
Cross application control and triggering
Manufacturer's recommended retail price (MSRP). The price shown does not include VAT. Prices and offers are only intended for entrepreneurs and not for private end consumers.
You may use the electronic signature via DocuSign to submit your information to enroll with the Rohde & Schwarz Customer Delegated Administration program. DocuSign processes the information provided according to their . The minimum system requirements for using the DocuSign system may change over time. The current system requirements are found
Terms & Conditions of the Prize Draw 10 years Rohde & Schwarz oscilloscopes
1. The prize draw “10 years Rohde & Schwarz oscilloscopes” (herein referred to as “Draw”) is organized by Rohde & Schwarz GmbH & Co. KG, Mühldorfstraße 15, 81671 Munich, Germany, Tel. +49 89 41 29 0 (herein referred to as “R&S).
2. All participators can register to the draw during January 01, 2020 to December 31, 2020 with their name, company name and business e-mail.
3. Participation is free of charge and not dependent on the purchase of goods or services.
4. The draw is only open to legal entities and only the legal entities are able to win the prizes. An individual person is not allowed to participate on its own name and its own account but as a representative of a legal entity filing the participation form in the name of and on behalf of the legal entity.
5. The prizes to win are 1 of 10 R&S®RTB2000 within the time frame January 1, 2020 to December 31, 2020:
Prize: 1x R&S®RTB2000 Digital Oscilloscope
6. The draw takes place at Rohde & Schwarz headquarters, Muehldorstrasse 15, 81671 Munich. The winner of the prizes will be informed by e-mail within 5 (5) working days.
7. The authorized representative of the legal entity shall inform Rohde & Schwarz about the acceptance of the price. In case of the denial of the acceptance, or no answer within two (2) weeks, a new winner will be drawn. If no winner can be determined within four (4) weeks, the draw ends and the prize forfeit.
8. R&S’ employees and members of their families and also person being familiar with the process of the draw and members of their families are excluded from filling the participation form.
9. No cash equivalent or exchange of prizes is allowed. Prizes are non-transferable. All taxes, levies, duties, fees and other charges levied in the participant´s country shall be borne by the participant.
10. Personal data will be processed only for the purpose of this prize draw and deleted four (4) weeks after the draw, if not agreed otherwise.
11. Any Participant who does not comply with these Terms & Conditions may be disqualified by R&S from this Competition. In such cases, prizes can also be withdrawn retrospectively. In case a prize is withdrawn retrospectively due to the non-compliance with these Terms & Conditions, it shall be returned by the respective participant at his cost to R&S’ address mentioned under Nr.1 and a new winner will be drawn.
12. The participants cannot claim the prizes of this draw and no legal recourse is permitted in this respect.
13. The draw and any contractual relationship arising therefrom between R&S and the respective participant shall be governed by and construed in accordance with the laws of Germany, without any recourse to the conflict of laws. The courts of Munich, Germany, shall have exclusive jurisdiction in case of any disputes arising directly or indirectly from the participation in this Competition.
* “fast delivery” inside 7 working days applies to the Rohde & Schwarz in-house procedures from order processing through to available ex-factory to ship.

