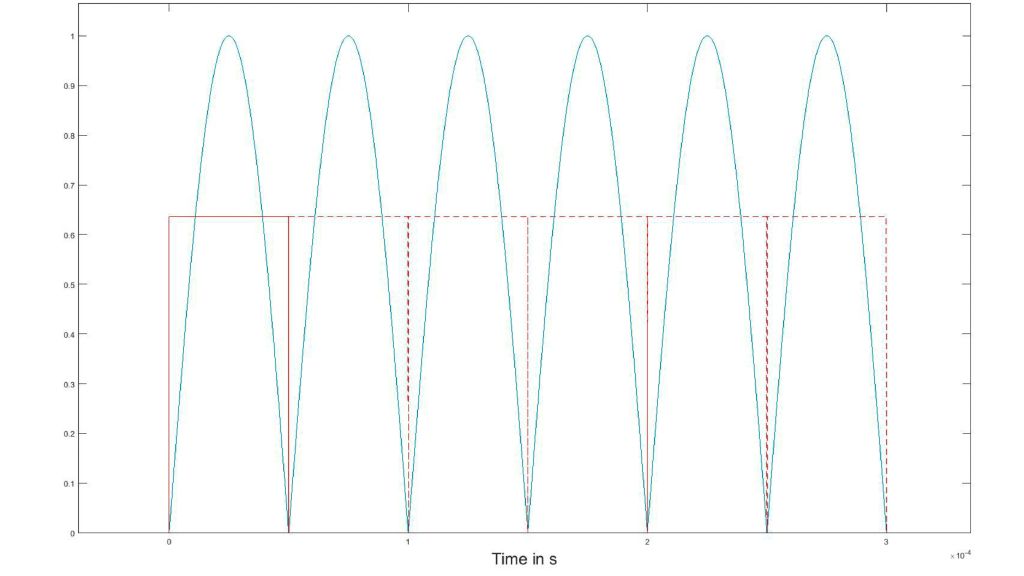
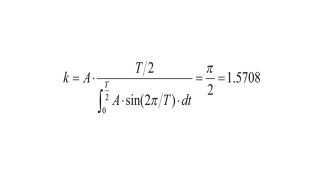Dieser Puls wird mit dem R&S®RTO analysiert. Abb. 2 zeigt die Gleichung für die Einhüllende in der R&S®RTO Math-Funktion (Formeleditor) mit einem Korrekturfaktor von k= π/2.
Um die beste Näherung für die Einhüllende zu erhalten, muss die Frequenz des Tiefpassfilters optimiert werden. Mit einer niedrigen Grenzfrequenz lassen sich Welligkeiten unterdrücken, jedoch ist der Einschwingvorgang langsam. Mit einer höheren Grenzfrequenz beschleunigt sich der Einschwingvorgang, es werden aber mehr Welligkeiten gemessen. In diesem Beispiel wird mit einer Grenzfrequenz von fcut = 50 MHz ein guter Kompromiss erreicht. Mit der bekannten Näherung trise = 0,35/fcut = 0,35/(50 MHz) = 7,0 ns lassen sich Einhüllende mit Anstiegszeiten größer als 7,0 ns analysieren.
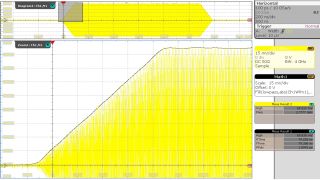
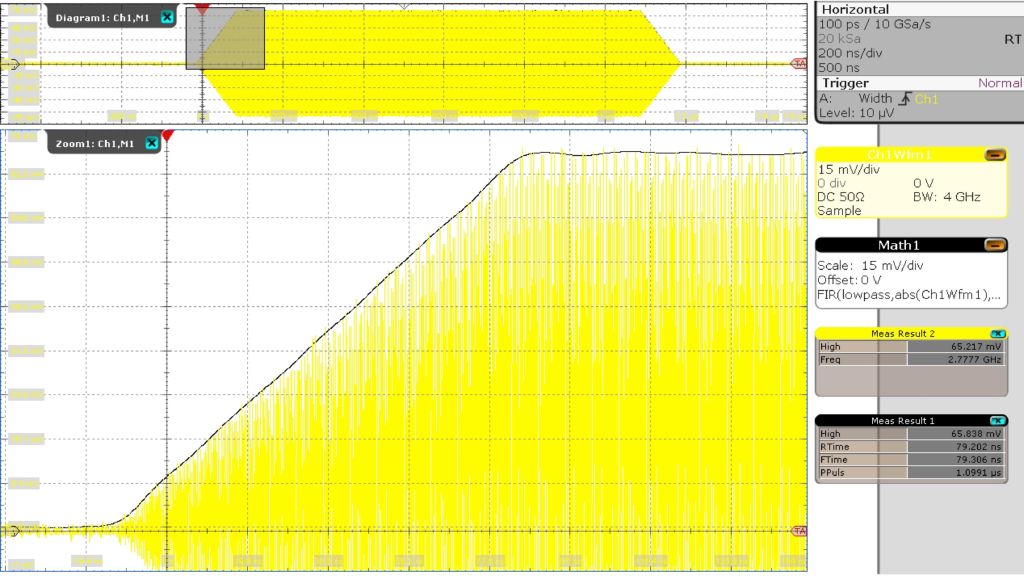
In Abb. 3 ist die gelbe Messkurve die modulierte Trägerwelle, die schwarze Messkurve repräsentiert die berechnete, korrigierte Einhüllende der Amplitudenmodulation.
Die Berechnung bei dieser Messung hat einen theoretischen Fehler von < 1,5 %, da der verwendete Tiefpassfilter eine Näherung des Mittelwerts der Integralberechnung ist. Die berechnete Einhüllende wird genutzt, um die Amplitude, Anstiegs-/Abfallzeit und Pulsdauer des modulierten Pulses korrekt zu messen. Das Kästchen mit dem Messergebnis „Meas Results 1“ in Abb. 3 rechts zeigt die endgültigen Messungen des HF-Pulses.
Das PRI wird mit dem History-Modus gemessen. Diese Messung wird in einer separaten Application Note beschrieben (Application Note 1TD02 „Erweiterte Signalanalyse mit dem History-Modus des R&S®RTO Oszilloskops“; M. Hellwig, T. Kuhwald).