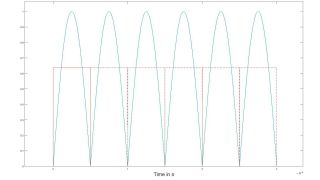
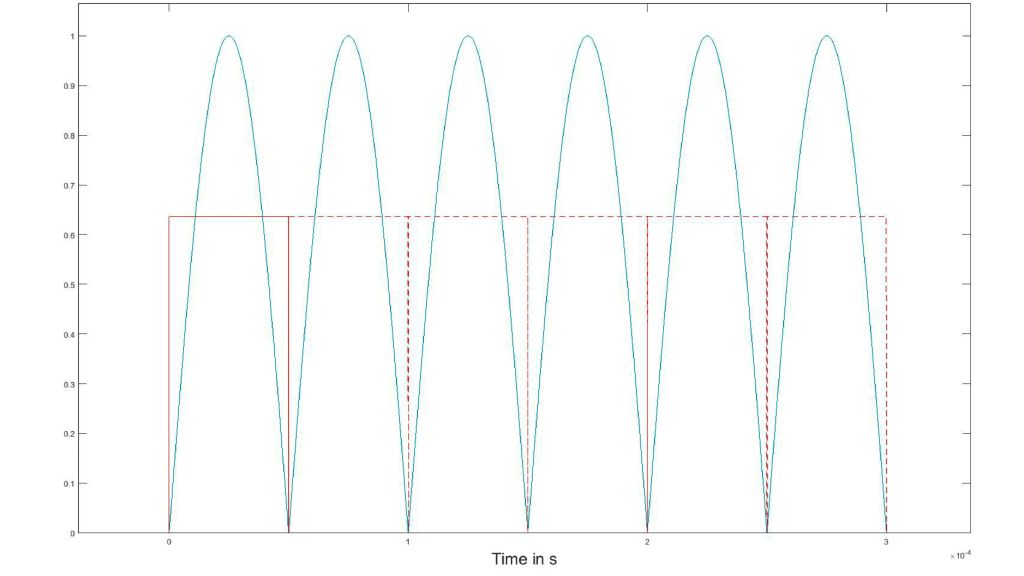
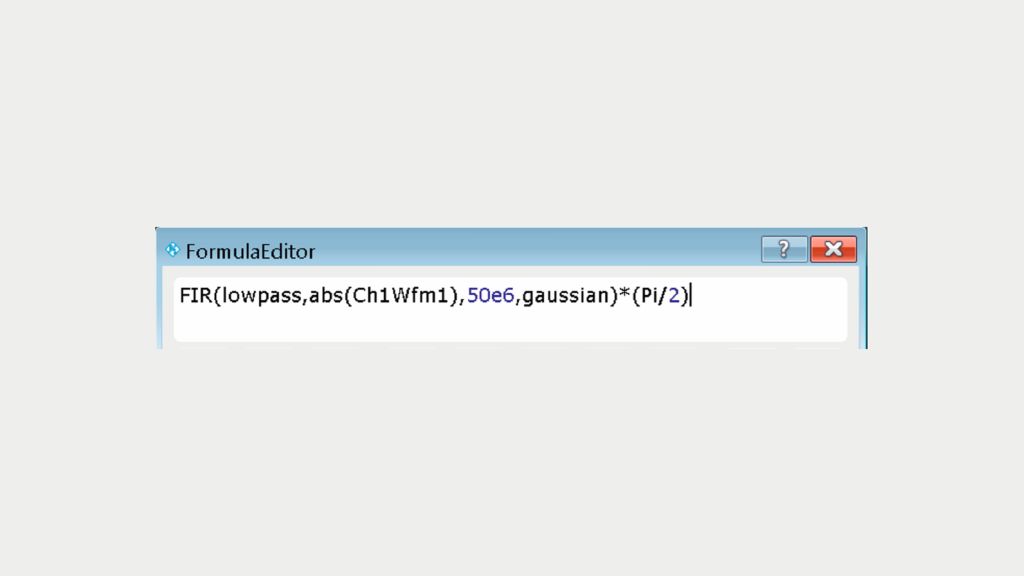
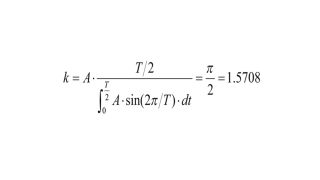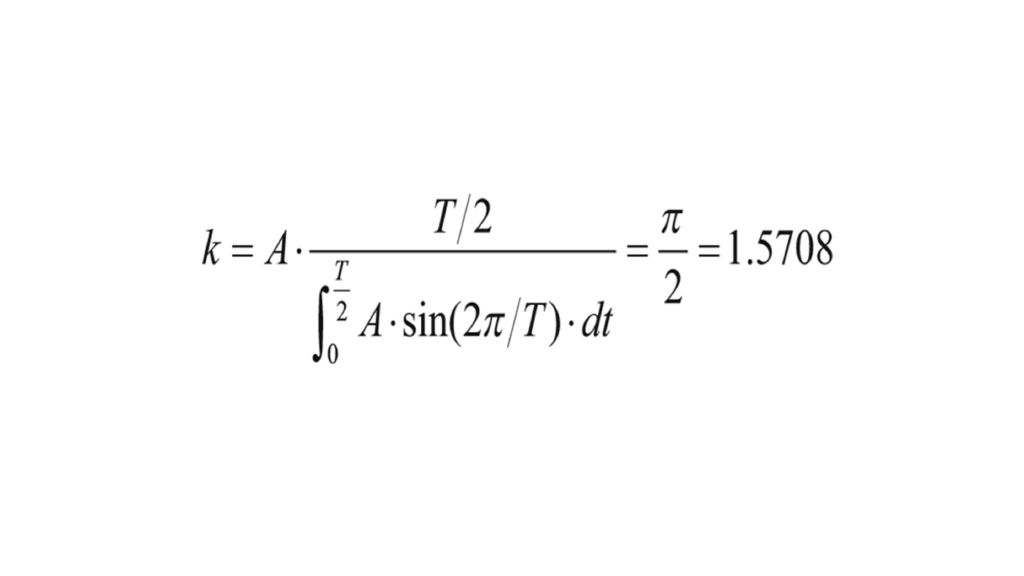This pulse is analyzed by the R&S®RTO. Fig.2 shows the equation for the envelope in the R&S®RTO math function (formula editor), which uses the correction factor k= π/2.
For the best approximation of the envelope, the frequency of the lowpass filter has to be optimized. With a low cutoff frequency, ripples can be suppressed, but the settling process is slow. With a higher cutoff frequency, the settling process is faster, but more ripples are measured. In this example, a good compromise of fcut= 50 MHz for the cutoff frequency is used. With the known approximation trise= 0.35/fcut = 0.35/(50 MHz) = 7.0 ns, envelopes with rise times greater than 7.0 ns can be analyzed.
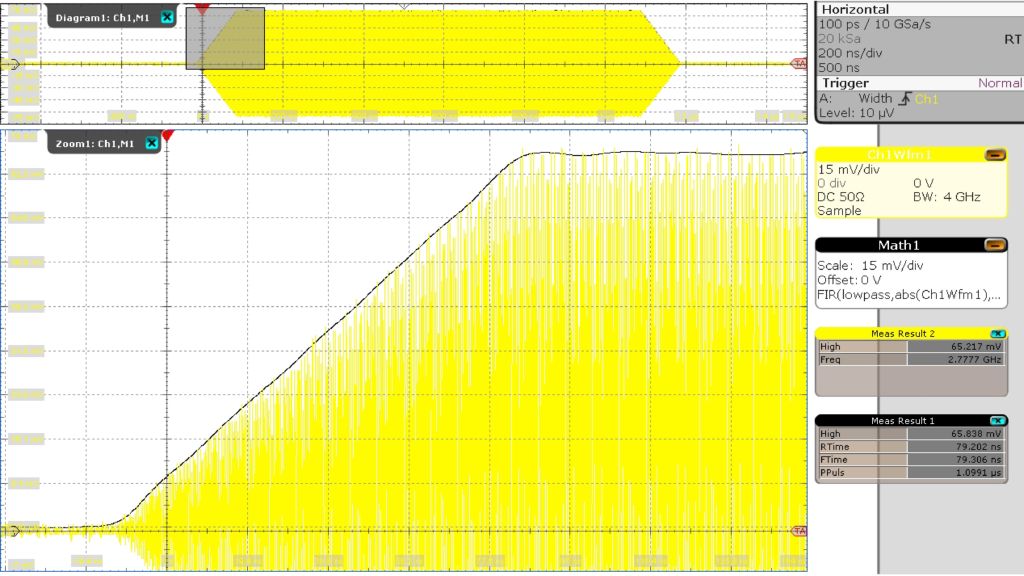
In Fig. 3, the yellow waveform is the modulated carrier wave and the black waveform represents the calculated, corrected envelope of the amplitude modulation.
The calculation in this measurement has a theoretical error of <1.5 % because the lowpass filter used is an approximation of the mean from the integral calculation. The calculated envelope is used to correctly measure the amplitude, rise/ fall time and pulse duration of the modulated pulse. The measurement result box “Meas Results 1” in Fig. 3 on the right shows the final measurements of the RF pulse.
The history mode is used to measure the PRI. This measurement is described in a separate application note (Application Note 1TD02 “Advanced Signal Analysis using the History Mode of the R&S®RTO Oscilloscope”; M. Hellwig, T. Kuhwald).