1-MHz- bis 50-GHz-Phasenrauschmessplatz mit direkter Abwärtsmischung und Kreuzkorrelation

Gregor Feldhaus und Alexander Roth

Rohde & Schwarz GmbH & Co. KG München, Deutschland

gregor.feldhaus@rohde-schwarz.com, alexander.roth@rohde-schwarz.com

Einleitung

Herkömmliche Phasenrauschmessplätze verwenden eine analoge Phasenregelschleife, um den Phasenversatz zwischen einem lokalen Referenzoszillator und dem Messobjekt zu ermitteln. Um die richtige Schleifenbandbreite und optimale Phasendetektoreigenschaften zu erreichen, ist eine tiefergehende Kenntnis des zu messenden Oszillators oder eine umfassende Vormessung der Eigenschaften des Messobjekts in Bezug auf Frequenzdrift erforderlich. Der Frequenzgang der analogen Phasenregelschleife muss bekannt sein oder kalibriert werden, um das Ergebnis der Nachmessung entsprechend zu korrigieren. Zudem erreichen analoge Phasenregelschleifen nur eine relativ schlechte AM-Rückweisung an den Phasenausgang – ein Effekt, der in letzter Zeit als Ursache für kreuzspektrale Einbrüche zunehmend in den Fokus gerückt ist [1].

Die Verlagerung des Phasendetektors in den digitalen Bereich verspricht einen deutlich vereinfachten Messaufbau und eine höhere Messgenauigkeit. Die spezifischen Eigenschaften der digitalen Bauteile sind vordefiniert und können mit höchster Präzision kompensiert werden. In [2] werden die HF-Wellenformen von Lokaloszillator und Messobjekt abgetastet, und auf dieser Basis wird der Phasenversatz zwischen den beiden Objekten digital berechnet. Die Trägerfrequenzen sind dabei jedoch beschränkt auf das Nyquist-Band des Analog-/Digitalwandlers. Mit Hilfe von zusätzlichen Mischern für Referenzoszillator und Messobjekt kann dieses Verfahren auch für den Mikrowellenbereich angewendet werden [3].

Bei dem in diesem Artikel beschriebenen alternativen Ansatz wird ein Lokaloszillator mit geringem Phasenrauschen für die direkte Abwärtsmischung des Messobjektsignals eingesetzt. Ein zweiter, unabhängiger Empfangspfad ermöglicht durch Kreuzkorrelation die Unterdrückung von nicht korreliertem Rauschen auf beiden Pfaden. Der auf dem Markt verfügbare R&S^®FSWP Phasenrauschmessplatz vereint die in diesem Artikel beschriebenen Verfahren und ermöglicht so Phasenrausch- und VCO-Messungen von CW-Quellen und Pulsquellen mit Frequenzen zwischen 1 MHz und 50 GHz[4].

Analoger Signalpfad

Abb. 1 zeigt die Komponenten des Phasenrauschmessplatzes mit zwei Kanälen für Kreuzkorrelationsmessungen.

Das an der Eingangsbuchse eingehende Hochfrequenzsignal wird hinter dem einstellbaren Dämpfungsglied in zwei separate Pfade aufgeteilt. Jeder Pfad verfügt über einen analogen I/Q-Mischer für die Umwandlung des Hochfrequenzsignals in zwei analoge niederfrequente Signale mit einer Phasenverschiebung von 90°. Die Lokaloszillatoren (LO) von Kanal 1 und Kanal 2 arbeiten auf Basis von zwei verschiedenen Referenztakten. Die Referenz von Kanal 2 ist über eine Phasenregelschleife mit einer Bandbreite von weniger als 0,1 Hz lose mit der Referenz von Kanal 1 verknüpft. So ist eine echte Kreuzkorrelation selbst für niedrige Frequenzoffsets von bis zu 0,1 Hz möglich.

Ob die Frequenz des Lokaloszillators oder die Frequenz des Messobjekts ausgewählt wird, hängt von den zu messenden Frequenzoffsets ab. Grundsätzlich gilt: je niedriger die Zwischenfrequenz (ZF) des resultierenden I/Q-Signals, desto besser das Rauschverhalten der nachgeschalteten Analog-/Digitalwandler. Demnach gälte eine Zwischenfrequenz von 0 als optimal. Bei freilaufenden Oszillatoren weicht die echte HF-Frequenz jedoch immer von der LO-Frequenz ab, was zu Oberwellen in der Differenzfrequenz führt. Eine Zwischenfrequenz von 0 wird also ausschließlich für die Messung von Frequenzoffsets von mehr als 1 MHz verwendet, da hier die Oberwellen der verbleibenden Frequenzabweichung so gering sind, dass sie sich nicht mehr negativ auf die Messung auswirken. Für Messungen von Frequenzoffsets unter 1 MHz wird eine Zwischenfrequenz von etwas mehr als 1 MHz verwendet, sodass die Oberwellen außerhalb des Messbereichs liegen.

Ein nicht zu vernachlässigender Faktor sind die in Abb. 2 dargestellten Störgrößen im Zusammenhang mit analogen I/Q-Mischern. Eine Abweichung von der gewünschten Phasenverschiebung von 90° sowie die unterschiedliche Verstärkung von I- und Q-Pfad führen zu einem I/Q-Ungleichgewicht (I/Q Imbalance), das auch eine AM/PM-Konversion zur Folge hat. Im Frequenzbereich tritt eine Spektrallinie an der gespiegelten Zwischenfrequenz auf. Der LO-Durchschlag fügt dem I/Q-Signal einen Gleichspannungsoffset hinzu. Abweichungen in Bezug auf Verstärkung und Phase sind für den Frequenzbereich des Geräts ab Werk kalibriert, während die Kalibrierung des Gleichspannungsoffsets vor jeder Messung durchgeführt wird. Die Kompensation dieser Effekte erfolgt im Pfad für die digitale Signalverarbeitung des FPGAs.

Mit diesem Empfängerkonzept kann in der Regel eine AM-Unterdrückung von 40 dB im Vergleich zu den mit herkömmlichen analogen Phasenregelschleifen erzielbaren 15 bis 30 dB erreicht werden, was die Wahrscheinlichkeit von kreuzspektralen Einbrüchen durch antikorrelierte AM/PM-Konversion verringert.

Digitaler Signalpfad

Die Auswahl des Analog-/Digitalwandlers (ADC) ist ausschlaggebend für die Performance von vollständig digitalen Phasendetektoren. Bei Systemen mit einer analogen Phasenregelschleife wird der Träger vor der Abtastung des Phasensignals unterdrückt, sodass nur der Rausch-Dynamikbereich außerhalb der Schleifenbandbreite berücksichtigt werden muss. Mit direkter Abwärtsmischung und Trägerabtastung muss der Analog-/Digitalwandler den kompletten Dynamikbereich des Eingangssignals abdecken.

Jeder der vier Analog-/Digitalwandler in Abb. 1 verfügt über vier parallele Kanäle mit einer Auflösung von 16 bit bei 100 Msample/s. Jeder Kanal erreicht ein Signal/Rauschverhältnis (SNR) von ungefähr 84 dB bezogen auf Vollaussteuerung. Durch die Mittelung der vier Kanäle wird das Signal/Rauschverhältnis um weitere 6 dB erhöht. Die Rauschleistung wird gleichmäßig zwischen Phasen- und Amplitudenrauschen aufgeteilt. Demnach ergibt sich der Beitrag des weißen Rauschens des Analog/Digitalwandlers für ein Eingangssignal mit Vollaussteuerung ohne weitere Kreuzkorrelationsverstärkung wie folgt:

L_ADC= (– SNR – 10∙log₁₀ (f_sample) – 3) dBc/Hz. (1)

Setzt man die oben angegebenen Zahlen ein, erhält man für ein optimal ausgesteuertes Eingangssignal einen Phasenrauschbeitrag von -173 dBc/Hz. Die externen Takteingänge des ersten und des zweiten Analog-/Digitalwandlerpaars basieren auf unterschiedlichen Referenzfrequenzen. Durch den Kreuzkorrelationsprozess wird das Phasenrauschen aufgrund des Referenztakt-Jitters des Analog/Digitalwandlers weiter reduziert.

Abb. 3 zeigt die digitale Signalverarbeitungskette, die sich hinter der I/Q-Abtastung verbirgt.

Um Kreuzkorrelationsmessungen zu ermöglichen, ist diese Struktur in einem FPGA zwei Mal vorhanden. Der Entzerrer am Eingang der Signalkette hat zwei Funktionen. Erstens kompensiert er den Frequenzgang der Filter im analogen Signalpfad getrennt für die I- und Q-Anteile. Zweitens kompensiert er die I/Q-Ungleichheit (I/Q Imbalance) und den Gleichspannungsoffset, die durch den analogen I/Q-Mischer eingebracht werden. Das entzerrte Signal kann über einen beliebigen Frequenzoffset verschoben werden, der an dem numerisch gesteuerten Oszillator eingestellt wird.

So wird das Spektrum auf der Trägerfrequenz zentriert. Ein nachgeschalteter Tiefpassfilter filtert die Signalanteile heraus, die außerhalb des betrachteten Spektrums liegen.

Pulsdetektor, Rauschsperre und Pulsfolgefrequenzfilter ermöglichen Messungen an Pulsquellen und werden bei Standard-Dauerstrichsignalmessungen überbrückt. Diese Funktion wird ausführlich in Abschnitt IV beschrieben.

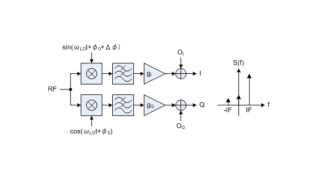
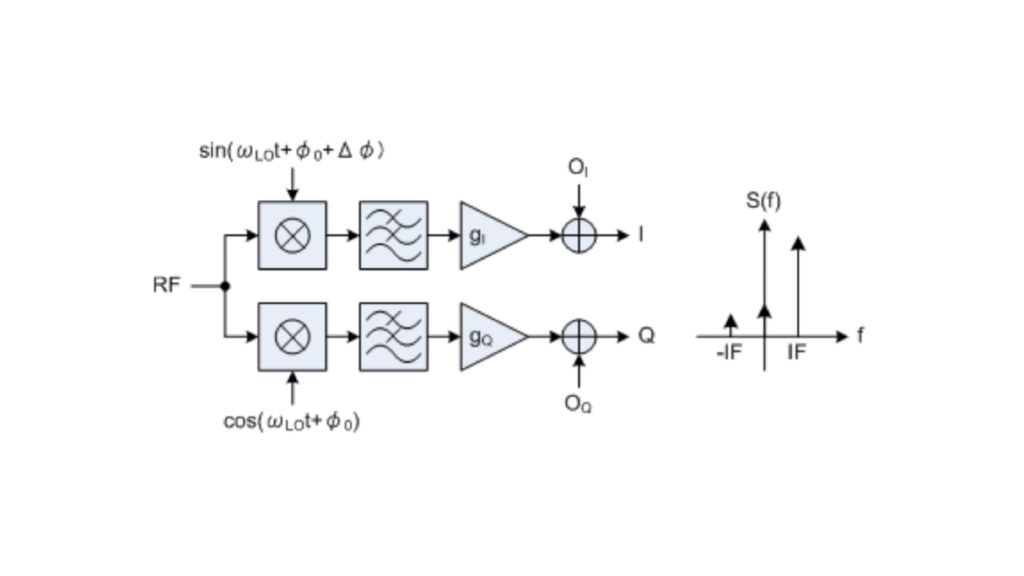
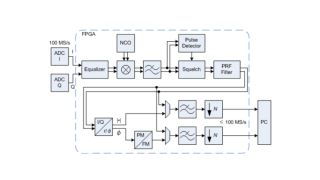
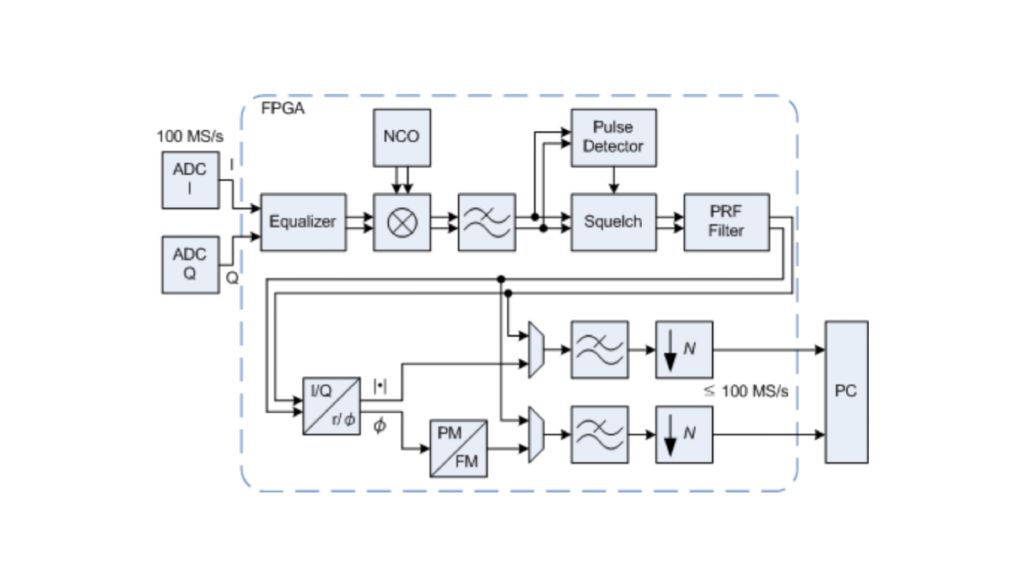
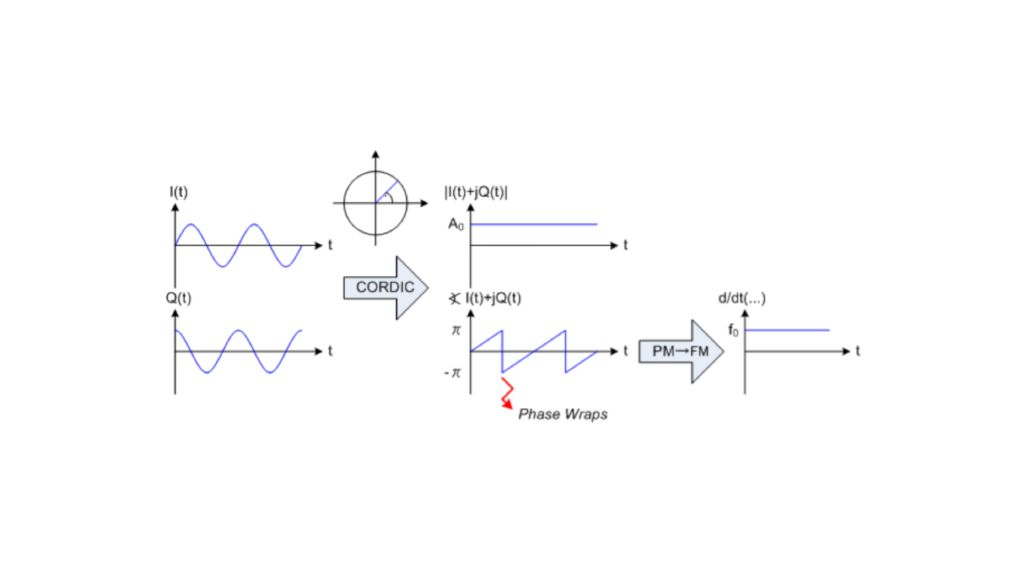
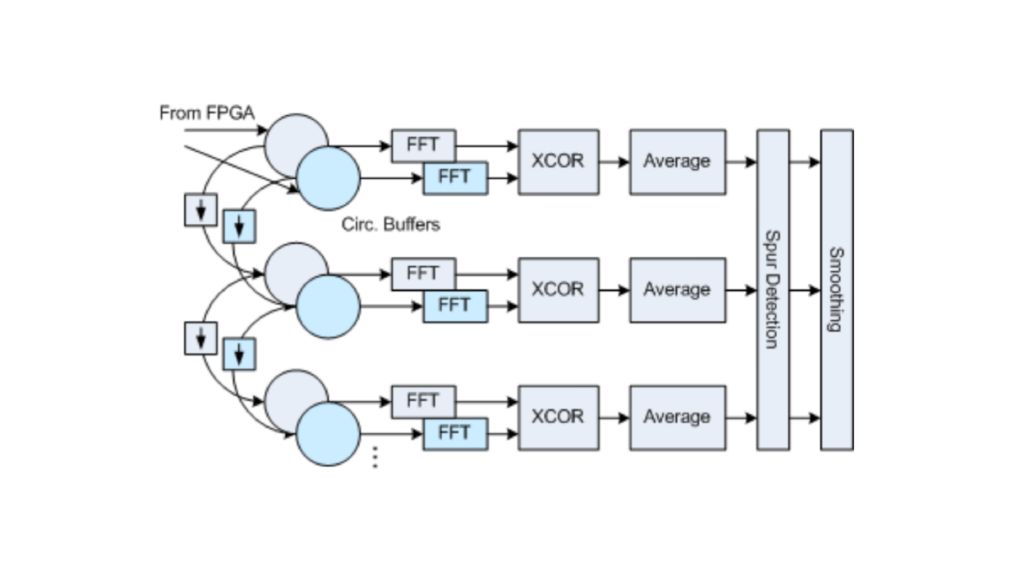
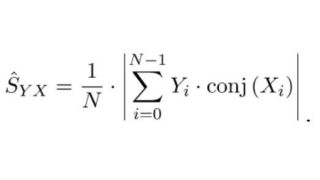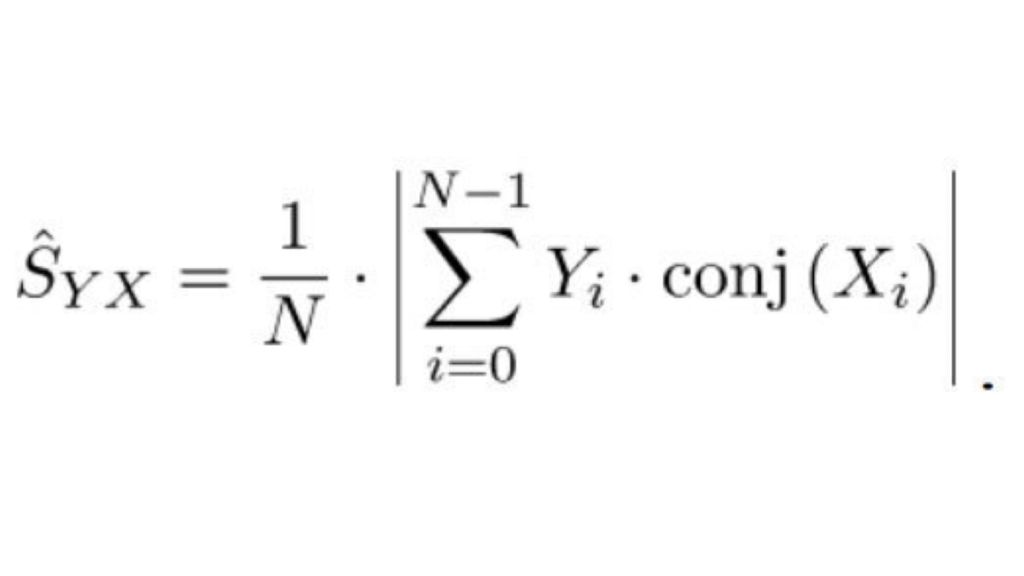Während die Signalverarbeitungskette bis zu diesem Punkt ähnlich wie bei Standardkonzepten für den digitalen Hörfunk aufgebaut ist, sind die folgenden AM- und FM-Demodulatoren ausschließlich bei dem neuen Ansatz zu finden, der die gleichzeitige Messung von Amplituden- und Phasenrauschen bis zu einem Frequenzoffset von 30 MHz ermöglicht. Für die Aufteilung des komplexen Basisband-I/Q-Signals in seine Betrags- und Phasenkomponenten wird ein CORDIC-Algorithmus (Coordinate Rotation Digital Computer) verwendet.

Das Betragssignal wird direkt für die Berechnung des Amplitudenrauschspektrums genutzt, während das Phasensignal vor der weiteren Verarbeitung in ein Frequenzsignal umgewandelt werden muss (siehe Abb. 4).

In der Regel weisen freilaufende Oszillatoren eine Drift gegenüber dem Lokaloszillator auf. Der unvermeidbare Frequenzoffset führt zu einer linear ansteigenden Phase mit Phasenumbrüchen (Phase Wrapping) bei ±π. Das Wrapping-Phasensignal ist nicht geeignet für weiteres Downsampling sowie die FFT-Verarbeitung. Eine offensichtliche Lösung wäre eine Rückkopplung zum vorgeschalteten numerisch gesteuerten Oszillator, um die Zwischenfrequenz auf 0 zu halten. Digitale Rückkopplungsschleifen können jedoch aufgrund von hohen Zeitkonstanten und schwierigen Anforderungen hinsichtlich der Bitzunahme problematisch sein. Bei dem hier vorgestellten Ansatz wird stattdessen ein Phasenableitungsblock als zuverlässige Feed-Forward-Struktur verwendet, und das PM-Signal in ein FM-Signal ohne Phasenumbrüche (Phase Wrapping) umgewandelt. Die langsame Frequenzdrift des Messobjekts wird in eine nieder- oder nullfrequente Komponente des FM-Signals umgewandelt, die die anschließende Filterung und FFT-Verarbeitung nicht beeinträchtigt.

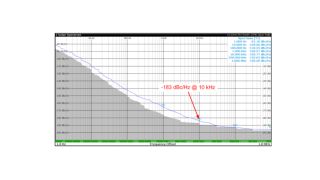
Analoge FM-Demodulatoren gelten als unsensibel für Phasenrauschmessungen nahe des Trägers, da der Frequenzgang des Demodulators mit 20 dB pro Dekade in Richtung Gleichspannung abfällt. Dieser Abfall muss bei der Messkurve der Nachmessung kompensiert werden, sodass jegliches weißes Rauschen, das hinter dem Demodulator auftritt, zum Beispiel durch Verstärker oder einen nachgeschalteten Analog/Digitalwandler, um 20 dB pro Dekade ansteigt. Digitale FM-Demodulatoren weisen dasselbe Verhalten in Richtung Gleichspannung auf. Im Gegensatz zu analogen Demodulatoren sind moderne FPGAs dank ihrer umfangreichen Ressourcen jedoch in der Lage, die erforderliche Steigerung der Messdynamik zu meistern. Die digitalen Dezimationsfilter, die dem FM-Demodulator in dem vorgestellten Ansatz nachgeschaltet sind, erzielen eine Sperrdämpfung von 220 dB. Somit ist der Abfall des Frequenzgangs des FM-Demodulators für 11 Dekaden abgedeckt! Die Signalbitbreite wird entsprechend erhöht, um sicherzustellen, dass jegliches Quantisierungsrauschen in jedem Fall unterhalb des FM-demodulierten Phasenrauschens liegt.

Für die digitalen AM- und FM-Demodulatoren müssen der Träger und der vollständige zweiseitige Messbereich innerhalb der Nyquist-Bandbreite des I/Q-Signals präsent sein. Der maximale über den Demodulatorpfad messbare Frequenzoffset liegt daher bei 30 MHz. Bei größeren Frequenzoffsets wird nur die Summe von Amplituden- und Phasenrauschen gemessen. In diesem Fall ermöglicht der digitale Signalpfad die Überbrückung des Demodulators und übermittelt die I/Q-Daten direkt an die nachgeschaltete Prozessoreinheit, wo die Standard-Spektrumberechnung erfolgt.

Phasenrauschmessungen an Pulsquellen

Der AM- und FM-Demodulatoransatz eignet sich ebenfalls für Phasenrauschmessungen an Pulsquellen ohne einen zusätzlichen Messaufbau. Im Rahmen einer Vormessung werden die Pulsparameter wie Pulspegel, Pulsbreite und Pulswiederholzeit ermittelt. Durch das Pulsen einer Signalquelle wird im Frequenzbereich ein Kammspektrum mit Wiederholungen umgekehrt proportional zur Pulsperiode erzeugt, wie in Abb. 5 gezeigt. Bis hin zur Hälfte der Pulsfolgefrequenz können so aussagekräftige Phasenrauschmessungen durchgeführt werden. Das Blockschaltbild in Abb. 3 enthält einen Pulsfolgefrequenzfilter, der alle Wiederholungsspektren außer der Hauptkeule abschneidet. Das Ausgangssignal des Filters entspricht einem Dauerstrichsignal und kann in dieser Form von AM- und FM-Demodulatoren verarbeitet werden.

Mit Hilfe der optionalen Kombination aus Pulsdetektor und Rauschsperre, die dem Pulsfolgefrequenzfilter vorgeschaltet werden, kann sämtliches Rauschen während der Pulspausen auf Null gesetzt werden. Dies bietet einen bemerkenswerten Vorteil gegenüber analogen Pulsfolgefiltern, die die Rauschleistung der Pulspausen ihrem Ausgangssignal hinzufügen. Die Differenz zwischen gepulster und nicht gepulster Hauptkeulen-Trägerleistung wird häufig als Pulse Desensitization Factor bezeichnet:

Pulse Desensitization = 20 ∙ log₁₀ (T_Breite / T_Rep) dB. (2)

Werden keine Gegenmaßnahmen getroffen, verringert sich das Phasen/Rauschverhältnis hinter dem Pulsfolgefrequenzfilter um diesen Faktor und bringt die Phasenrauschmessung näher an das Grundrauschen des Geräts. Das Setzen der Rauschleistung der Pulspausen auf Null hingegen reduziert die Rauschleistung in folgendem Maße:

Rauschgewinn = 10 ∙ log₁₀ (T_Breite / T_Rep) dB. (3)

Durch die Kombination der beiden Effekte wird die Aussteuerbarkeit des hier vorgestellten Ansatzes für die Pulsmessung um 10 ∙ log₁₀ (T_Breite / T_Rep) verringert, was nur der Hälfte des gesamten Pulse Desensitization Factors aus (2) entspricht.

Kreuzkorrelation

Die Kreuzkorrelation und die Berechnung der Ergebniskurve erfolgen auf einem Standard-PC-Prozessor, der über PCI Express mit dem FPGA verbunden ist. Der Frequenzbereich wird logarithmisch in Abschnitte unterteilt, die ungefähr eine halbe Dekade abdecken, zum Beispiel 1 Hz bis 3 Hz, 3 Hz bis 10 Hz und so weiter. Abb. 6 zeigt die verschiedenen Verarbeitungsschritte. Die AM- und FM-Signale vom FPGA werden in Ringspeicher eingespeist. Die Signale werden ständig weiter herunterdezimiert, um die parallele Verarbeitung mehrerer Frequenzabschnitte mit unterschiedlichen Auflösebandbreiten zu ermöglichen. Jeder Abschnitt wird mittels FFT in den Frequenzbereich umgewandelt. Die tatsächliche Kreuzkorrelation der beiden unabhängigen Signalpfade erfolgt mit Hilfe konjugierter komplexer Multiplikation der FFT-Ergebnisse und des anschließenden Mittelungsblocks. Das geschätzte Leistungsdichtenspektrum für N Korrelationen zwischen der FFT des ersten Kanals X und der FFT des zweiten Kanals Y kann wie folgt ausgedrückt werden:

Kreuzkorrelation verringert den Phasenrauschbeitrag von nicht korrelierten Rauschsignalen, also dem Rauschen, das im Gerät hinter dem Teiler am HF-Eingang auftritt, um 5∙log₁₀(N) dB, wobei N die Anzahl der Korrelationen ist. Solange das nicht korrelierte Rauschen des Geräts größer als das korrelierte Rauschen des Messobjekts ist, verringert sich das Ergebnis von (4) entsprechend. Wenn das korrelierte Rauschen beginnt, das gemittelte nicht korrelierte Rauschen zu übersteigen, festigt sich das Ergebnis von (4) und wird zum tatsächlichen Messergebnis.

Das Gerät kann die Messung automatisch stoppen, wenn ein bestimmter Abstand zwischen dem gefestigten Ergebnis von (4) und dem theoretisch maximal möglichen Abfall für nicht korrelierte Eingangssignale erreicht ist. So kann unnötige Messzeit für Kreuzkorrelationen eingespart werden, die das Endergebnis nicht weiter verbessern würden.

Performance des Geräts

Die Performance eines Phasenrauschmessplatzes mit Kreuzkorrelation wird definiert durch das Eigenrauschen des Geräts und die Messgeschwindigkeit bei der Durchführung einer bestimmten Anzahl an Kreuzkorrelationen. Die in den vorgestellten Messplatz integrierten Lokaloszillatoren sind den meisten auf dem Markt verfügbaren Generatoren und Quellen hinsichtlich des Phasenrauschens überlegen. Abb. 7 zeigt das typische Grundrauschen des Systems bei einer Messzeit von 10 Sekunden.

Bei der Messung von Frequenzoffsets von bis zu 1 MHz hängt die Messgeschwindigkeit in erster Linie von der Zeit ab, die für die physikalische Erfassung zum Erreichen einer bestimmten Auflösebandbreite (RBW) für eine gegebene Anzahl an Kreuzkorrelationen erforderlich ist. Bei Verwendung eines Blackman-Harris-Fensters für die FFT und einem Overlap Factor (Überlappungsfaktor) von 0,75 lässt sich die Erfassungszeit wie folgt ausdrücken:

T_Erfassung = 2,0 / RBW ∙ (1 + 0,25 (N_XCORR-1)). (5)

Für höhere Frequenzabschnitte erfasste Daten werden für die gleichzeitige Berechnung von darunterliegenden Abschnitten verwendet. Die Kombination aus herausragender HF-Performance und intelligenter Signalverarbeitung ermöglicht eine unschlagbare Messgeschwindigkeit. Abb. 8 ist das Ergebnis einer Phasenrauschmessung eines Oszillators der Spitzenklasse, die innerhalb von nur zwei Minuten durchgeführt wurde. Dieser Oszillator wurde im United States National Institute of Standards and Technology (NIST) kalibriert, um die Genauigkeit des Messergebnisses zu verifizieren.

Referenzen

[1] Nelson, C.W.; Hati, A.; Howe, D.A., „A collapse of the cross-spectral function in phase noise metrology“, Rev. Sci. Instrum., Vol. 85, 2014

[2] Grove, J. et al., „Direct-digital phase-noise measurement“, Proc. of Frequency Control Symposium and Exposition, 2004, pp. 287-291, 23-27 Aug. 2004.

[3] Parker, S.R.; Ivanov, E.N.; Hartnett, J.G., „Extending the Frequency Range of Digital Noise Measurements to the Microwave Domain“, IEEE Transactions on Microwave Theory and Techniques, Vol. 62, No. 2, pp. 368-372, Feb. 2014.

[4] Rohde & Schwarz, „R&S^®FSWP Phasenrausch- und VCO-Messplatz“, Produktbroschüre, 2015.

© 2016 IEEE. Die Nutzung dieser Inhalte ist zum persönlichen Gebrauch gestattet. Für jeden anderen Gebrauch in allen aktuellen oder zukünftigen Medien, einschließlich Nachdruck/Neuauflage dieser Inhalte für Werbe- oder Vermarktungszwecke, Erschaffen neuer gemeinschaftlicher Werke, Weiterverkauf oder Weitergabe an Server oder Listen oder Wiederverwendung jeglicher urheberrechtlich geschützter Bestandteile dieses Werks in anderen Werken, ist die Zustimmung von IEEE erforderlich. DOI: 10.1109/EFTF.2016.7477759